Quantifying Risk-to-Mission: Lessons from Operation Eagle Claw
From War Quants: This week we welcome guest contributor Ryan Helm to introduce a critical historical lesson in the importance of robust quantitative analysis to operational planning. The failure of Operation Eagle Claw forms a fundamental touchstone in the military operations research (OR) community, and versions of this case study are still taught to analysts in training in the OR curriculum at the Naval Postgraduate School. We are excited for the opportunity to share derived insights with a wider audience. We have also linked some foundational community analysis on Operation Eagle Claw at the bottom of this article.
Is a 35% probability of failure acceptable for a high-stakes hostage rescue mission?
According to the declassified Holloway Report on the Iran hostage rescue operation of 1980, this is exactly the risk unknowingly assumed by the planning team for Operation Eagle Claw. Due to a fundamental miscalculation regarding how many helicopters should be sent, every advisor and commander in the operational chain of command, including the Chairman of the Joint Chiefs and the President of the United States, approved a rescue mission that had only a 65% chance of even arriving at the first staging area successfully. Many years later, when asked if there was anything he would have done differently during his presidency, President Carter responded, "I wish I would have sent one more helicopter to get the hostages." In this article, I will share two classic operations research lessons: how varied numbers of helicopters would have affected the likelihood of Operation Eagle Claw’s success and the importance of communicating risk-to-mission through probabilities.

Context For a Complex Rescue
During the Iranian Revolution, armed Iranian students captured 53 American hostages at the U.S. Embassy in Tehran. Rescue mission planning began on 4 November 1979 and ran for nearly five and a half months. While the U.S. was pursuing diplomatic solutions, the rescue team faced a myriad of complex planning challenges, many of which stemmed from Tehran’s geographic isolation. To insert a hostage rescue team from the Gulf of Oman via the USS Nimitz, U.S. military helicopters would first need to complete a nearly 750 nautical mile flight to reach the hide site, Desert Two. This distance exceeded the helicopters' range, necessitating a rendezvous with C-130s at an intermediate staging area, Desert One, to refuel and embark the assault force. Finally, after a second flight to reach Desert Two, four RH-53Ds would need to wait until nightfall and launch again to conduct the rescue.
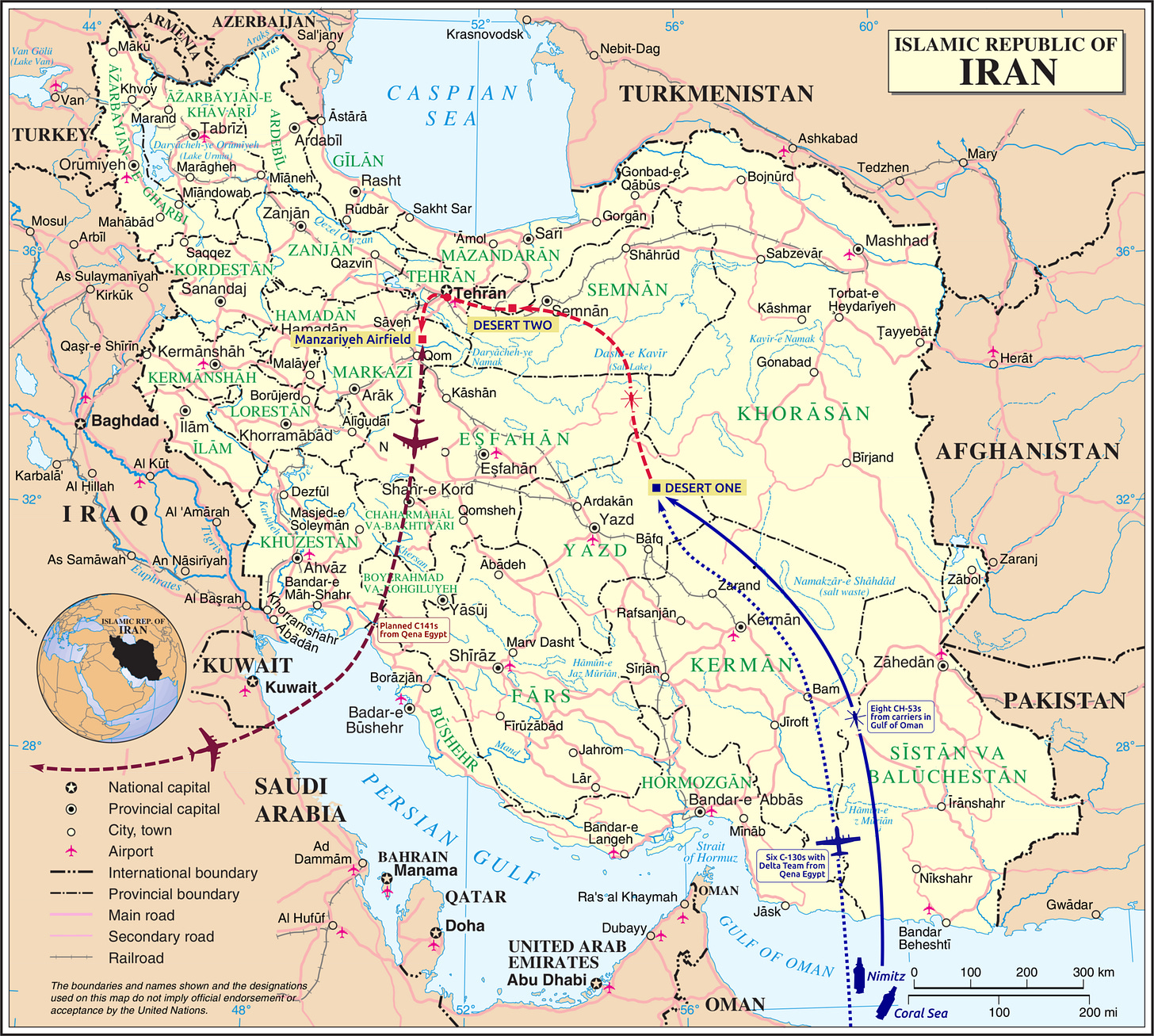
How Many Helicopters to Send?
At the time of the operation, the RH-53D had a fleet-wide mission capability rate of 74.0%. In an attempt to compensate for the potential failure of the rescue aircraft, military planners reasoned that if four helicopters needed to launch from Desert Two, five helicopters would need to arrive at Desert Two, six would need to arrive at Desert One, seven would need to be operational at launch, and eight helicopters would need to be staged aboard the USS Nimitz. In other words, if approximately three-quarters of RH-53D aircraft were mission capable, then with eight aircraft launched, six aircraft could be expected to reach Desert One on average.
The reasoning of Operation Eagle Claw’s military planners:
74% mission capability rate * 8 helicopters launched = 5.92 helicopters expected to reach Desert One
Beware of Averages in Planning
Unfortunately, hindsight reveals that the rationale of multiplying the average fleet-wide mission capability rate by the number of aircraft launched fails to accurately capture risk. While intuitive, averages don't sufficiently account for the independent randomness inherent to each aircraft or communicate a likelihood of success. To quantify and understand risk-to-mission, commanders must consider probabilities of success, not average outcomes or expected values.
To better understand the impact of average-based planning assumptions, let's quantify the probabilities of success for different launching scenarios. For the scope of this article, I define mission success as six or more helicopters reaching Desert One in mission-capable condition. I will also assume that the determination of each helicopter's operational readiness is an independent event, like a coin toss. These events are called Bernoulli trials in probability theory, where the probability that a certain number of events achieve a desired outcome is modeled with a binomial distribution.
To quantify and understand risk-to-mission, commanders must consider probabilities of success, not average outcomes or expected values.
In this scenario, calculating the probability of at least six helicopters reaching Desert One is identical to calculating the probability of getting six or more heads in eight independent coin tosses, except instead of a 50/50 coin probability, we use the 74% mission capability rate of the RH-53D helicopters. The table below quantifies the risk-to-mission for potential flight plans under these assumptions, illustrating how the number of helicopters launched dramatically affects the likelihood of mission success.
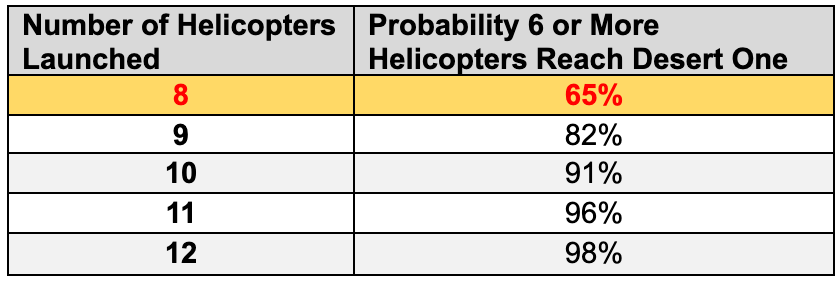
This analysis highlights the rescue plan’s inherent vulnerability: with eight helicopters launched, there was only a 65% chance that six mission-capable helicopters would reach Desert One. Even increasing the number of launched helicopters to ten would have raised the probability to just 91%.
Execution
The Holloway investigation found that after the launch of eight helicopters on the evening of 24 April 1980, Helicopter #6 registered cockpit warnings for compromised rotor blade integrity, forcing the crew to abandon the aircraft. Vital flight and navigation instruments failed on Helicopter #5, forcing a return to the USS Nimitz. Helicopter #2 encountered a partial hydraulic failure but continued to Desert One. At this point, only five helicopters reached Desert One in operational condition (below the planned no-go threshold), and the mission was aborted.
With eight helicopters launched, there was only a 65% chance that six mission-capable helicopters would reach Desert One.
Aftermath
During refueling for withdrawal from Desert One, a maneuvering RH-53D impacted one of the C-130s, igniting ammunition and fuel tanks onboard. Both aircraft were destroyed, and five Airmen and three Marines lost their lives. All remaining helicopter crew and ground forces retrograded on the unaffected C-130s. The hostages were not released until 20 January 1981, and a commission led by Admiral Holloway was ordered to investigate the rescue operation. The Holloway Report identified the need for better integration among the services and the acquisition of a long-range vertical lift capability, leading to the establishment of the V-22 tiltrotor program in 1982 and the creation of U.S. Special Operations Command (USSOCOM) after the passage of the Goldwater-Nichols Act in 1986.
"Planning was adequate except for the number of backup helicopters and provisions for weather contingencies. A larger helicopter force and better provisions for weather penetration would have increased the probability of mission success."
—Excerpt of findings from the Holloway Report
Conclusion
Operation Eagle Claw highlights the critical importance of quantifying risk-to-mission and building resilience into mission plans. By relying on averages rather than probabilities, planners underestimated the likelihood of failure, and this vulnerability ultimately resulted in an aborted mission and a tragic loss of life. These lessons extend beyond a single operation. Effectively quantifying and communicating risk is an essential tool for commanders and planners, enabling more informed decisions in complex and high-stakes environments.
Further Reading on Operation Eagle Claw and Military Readiness:
Moving Toward A Holistic, Rigorous, Analytical Readiness Framework
Military Readiness Toolkits from the MORS Community of Practice in Probability Management
The Flaw of Averages by Sam L. Savage.
Read More of Our Work Here:
FPV Attack Drone Proliferation: Unfreezing Conflict in Syria
FPV Math: Precision Mass for 21st-Century Warfare
Capability Analysis: AI Machine Guns for Drone Short-Range Air Defense
Carrier 2.0: The Drone Carrier Revolution
The views and opinions expressed on War Quants are those of the authors and do not necessarily reflect the official policy or position of the United States Government, the Department of Defense, or any other agency or organization.




Great analysis. The Binomial distribution has scary maths to non mathsy people, but Excel and Google sheets etc has the function plumbed in, so it's just a question of entering probability of success and number of trials in, and the function does the rest.