How Much CUAS is Enough? A Swarm Equation Approach to Kinetic Tactical Defense
Kinetic CUAS
Small UAS systems pose new threats to tactical units on the battlefield, and the danger is amplified when drones attack in swarms. For tactical ground units, kinetic terminal defense is often the final protective layer in a CUAS architecture, and arguably the most critical. Other countermeasures, such as electronic warfare (EW), can be more widely effective and thus an essential part of the overall architecture. However, capabilities like EW will be subject to the cat-and-mouse game of innovation and counter-innovation of both tactics and technology. When such countermeasures fail, it is essential to have the final protective measures in place—stopping incoming UAS by physically rendering it unable to perform its mission through kinetic force.
There are a plethora of kinetic CUAS systems and ideas on the market. Solutions range from nets and shotguns to computer-aided aiming devices and AI-enabled machine guns. Some of these solutions, such as shotguns and computer-aided aiming devices, would be employed at the individual troop level. In contrast, others, like an AI-enabled machine gun, would be an asset assigned to protect a unit, such as at the squad, platoon, or company level. The type of solution or mix of solutions chosen may be more or less appealing depending on the tactical unit’s mission and method of employment. However, when selecting the right solution, it is helpful to understand the level of protection provided and make informed trades against other relevant attributes such as size, weight, sustainability, mobility, and magazine depth, among others.

Framing the Problem
Consider equipping a rifle squad with CUAS capabilities. It may be desirable to equip the squad with individual-level protection, such as a computer-aided aiming device, but does everyone in the squad need one? How many is enough? One per fire team or one per person? How does the level of protection of these individual solutions compare to providing the squad with an AI-enabled machine gun? These questions also apply to higher echelons and other tactical formations. This article introduces a quantitative model for addressing these critical questions.
Drone Swarms
Before proceeding, it is essential to define the term 'swarm' in this context. Some definitions of the term 'drone swarm' hinge on the method of control and behavior of the drones, such as full autonomy or drones in the swarm being aware of the other drones' actions and movements, which creates emergent behavior within the drone formation. These distinctions are important, but for the purposes of this discussion, a swarm is defined as any group of drones that fly together in an echelon of two or more. The defender's perspective shapes the definition in this context. When employing kinetic defense, the method of control is of little importance to the defender. Whether all the drones are autonomous or have a one-to-one drone-to-operator ratio is of less consequence than whether your CUAS can engage the volume of incoming drones.
The Model
The nature of kinetic CUAS is reminiscent of naval missile combat, where ships must plan to intercept incoming missile threats. Wayne Hughes’ famous salvo equations eloquently modeled this form of combat, and as such, these equations serve as a starting point for this CUAS model, where the salvo equations are modified to become swarm equations.
In the swarm equations, we are ultimately concerned with the number of attacking drones the defender can shoot down and the number of hits the remaining drones can inflict. The parameters in the base swarm equations are given below:
Based on these model parameters, the number of drones shot down in an attacking swarm, S, is given as:
This leaves the remaining drones to hit their target.
This model enables comparisons between the levels of protection afforded by different systems, and allowing CUAS practitioners to make informed decisions about the tradeoffs in system capabilities. The model can provide insight into considerations such as minimum protection levels, the swarm saturation point of CUAS defense, and the comparative effectiveness of squad versus individual systems. However, the model does not capture the impacts of these systems on other missions, e.g., the mission opportunity cost of an individual carrying an individual CUAS system versus another weapon like a light machine gun.
Some key assumptions of the model are as follows.
CUAS shooters have perfect target discrimination and can evenly distribute kinetic effects to all targets. This means that if there are more drones incoming than defending systems, the defending systems will engage individual drones without firing on the same drone. However, if there are more defensive systems than drones, there will be duplicate engagements, increasing the probability of intercepting all targets.
Drones in an incoming swarm arrive close enough in time to be simultaneous to the defender.

Bullfrog from Allen Control Systems. AI automated tracking and firing M240 for CUAS. Image from Allen Control Systems.
Application to a Rifle Squad
To demonstrate the utility of the model, we will consider its application in modeling the CUAS systems in a base tactical unit, a 13-person rifle squad. Force planners must make decisions on the level of protection appropriate to this formation. The easy answer is to give them maximum protection, but depending on the CUAS system's size and cost, it may detract from the other missions and functions the rifle squad is intended to carry out.
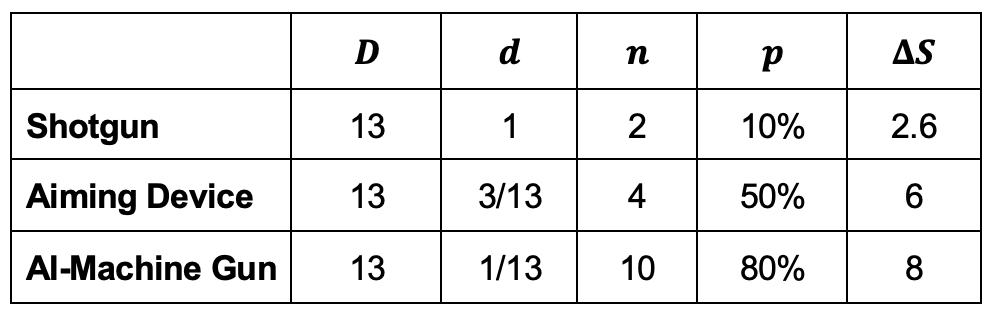
In this context, let us consider three kinetic CUAS squad packages. Note that parameters chosen for the model are for demonstration purposes only and are not meant to reflect empirical knowledge of system performance.
All members of the squad receive a shotgun. Each squad member is capable of firing two shots at an incoming swarm with a 10% chance of hitting with each shot.
Each fireteam (three fireteams in the squad) has a member given a CUAS computer-aided firing device on their service rifle. This means that 3 of 13 squad members have a CUAS system capable of engaging 4 drones in an incoming swarm with a 50% probability of kill in each engagement.
The squad is equipped with a single AI-enabled machine gun for CUAS. This system can engage up to 10 drones with an 80% probability of kill.
The table above summarizes the model parameters for each CUAS package and the resulting S, or the expected number of drones that the package can shoot down from an incoming swarm.
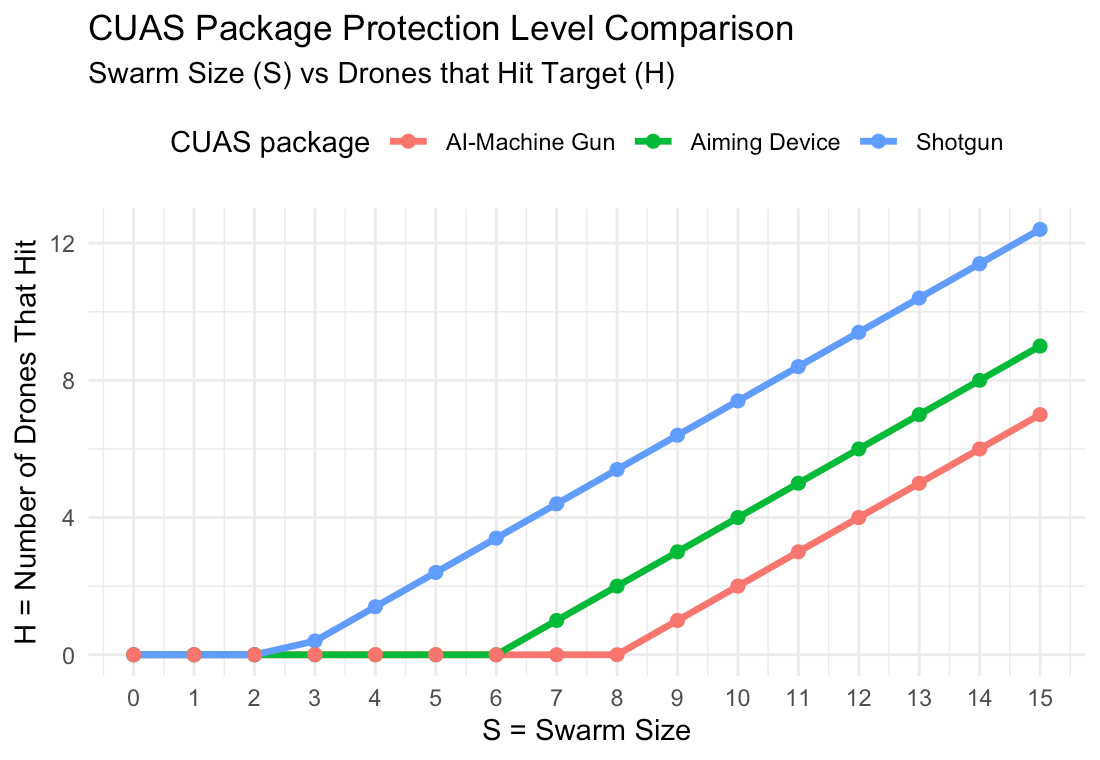
We can then use this data to see how many drones would still be able to hit their target, H, across various swarm sizes as shown in the graph below.
Keeping in mind that these are notional performance parameters, we can make some observations. For small swarms, all three packages can prevent any drones from getting through. As the swarm size grows past each package’s kill capacity, H begins to rise sharply—first for the shotgun package, then the aiming devices, and last for the AI-machine gun. While the parameters are made up, this simple model provides a way to compare various CUAS systems. To validate actual system performance, empirical data collection from field testing systems and various CUAS packages would be required.
The swarm equation model presented here is intentionally simple: it uses expected values to estimate the number of drones defeated (K) and those that get through (H) based on force size, engagement capacity, and probability of kill. That simplicity makes it easy to compare systems and visualize saturation points, but it also leaves room for refinement.
Further Validation
Validation against real-world tactics is a key next step. The model assumes all defenders can bring their CUAS system to bear on the swarm and that the swarm arrives simultaneously. In practice, dispersion—either of the defenders or the attacking drones—will affect engagement opportunities. A dispersed defending element might not be able to concentrate fire on the same portion of a swarm; conversely, a dispersed swarm might saturate multiple points at once, reducing the local density of defenders.
The deterministic outputs shown here can also be extended to stochastic versions. A stochastic approach would better capture variance and risk beyond just expected values.
Another avenue is to include mixed CUAS packages in the analysis. A rifle squad might combine an AI-enabled machine gun with a few computer-aided aiming devices, or distribute handheld systems across key positions. Modeling combinations would help identify optimal mixes for different expected swarm profiles and cost constraints.
Also, it may be useful to compare CUAS protection at echelon. Layered defense at higher echelons—platoon, company, or battalion—can incorporate multiple engagement zones, from long-range interceptors down to individual weapons. The swarm equation could be adapted to model each layer in sequence, showing how higher-level assets thin the swarm before it reaches the squad’s terminal defenses.
The bottom line: this model isn’t a substitute for field testing, but it is a fast, quantitative way to explore the trade space, set baseline requirements, and guide live-fire validation. Whether deciding how many systems to issue per squad, how to mix different CUAS capabilities, or how to layer them from squad to battalion, the framework helps shift the discussion from guesswork toward data-driven force design.
The views and opinions expressed on War Quants are those of the authors and do not necessarily reflect the official policy or position of the United States Government, the Department of Defense, or any other agency or organization.




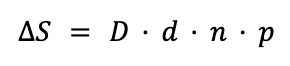

Nice job, dude! Now, what happens when you introduce stochastic variation (not just expectations)? Or if the swarm attacks in waves rather than a simultaneous burst? Also, how might degradation, sensor error, or mobility constraints shrink your effective kill capacity?
Gimme that sensitivity test! In practical use I’d love to see a sensitivity study or empirical fit of the model to actual test data. But even as a toy model, it moves the debate from intuition toward metrics.
The outcomes from the probability in your eqn will likely follow the binomial distribution so you will get times when you bring down more drones than you expect and others where you bring down less if any drones...